Photo of Jan Kurkofka

Dr. Jan Kurkofka

DFG Principal Investigator
Department of Mathematics
University of Hamburg
Bundesstraße 55, Room 229
20146 Hamburg, Germany

firstname.lastname
the-sign uni-hamburg.de

News

Selected Publications

Funding

Teaching

  • Full-time research on my DFG project (since Summer 2026, Hamburg)
  • Linear Algebra I (Winter 2025/26, Freiberg)
  • Algorithmic and Structural Graph Theory II (Summer 2025, Freiberg)

Teaching in previous semesters

Outreach

  • Spring academy for pupils, Freiberg, March 2025, voted best talk by the pupils. (Slides, in German)
  • Ruth Court Mathematics Society, King's High School, Warwick, January 2024. (Slides)
  • Birmingham Popular Maths Lecture, November 2023. (Slides)

Selected talks

  • SIAM Conference on Discrete Mathematics, San Diego, June 2026 (invited mini-symposium). (Slides)
  • Algebra and Combinatorics Seminar, Leipzig, June 2026 (invited).
  • SODA, Vancouver, January 2026.
  • Bertinoro Workshop on Algorithms and Graphs, October 2025. (Slides)
  • Plenary lecture, Ukrainian Summer School in Combinatorics, Freiberg, September 2025. (Slides)
  • Algebra-Geometry-Combinatorics Seminar, TU Dresden, January 2025 (invited). (Slides)
  • Topology Seminar, University of Pittsburgh, February 2024 (invited).
  • FOCS, Santa Cruz, November 2023. (Slides)
  • CanaDAM, Winnipeg, June 2023 (invited mini-symposium). (Slides)
  • Cambridge Combinatorics Seminar, November 2021 (invited).

Research interests

My research interests include Graph Minor Theory, Connectivity Theory, Topological Graph Theory, Infinite Graph Theory, and applications in Theoretical Computer Science and Group Theory. Here are some ongoing and recent projects:

A 2-connected graph and its cactus-decomposition

Cactus-decompositions for all levels of connectivity

Decomposing graphs into highly connected regions is a foundational method in Graph Minor Theory, and Connectivity Theory more broadly. Explicit solutions to the following problem for any k would be tremendously useful for computing excluded minors: Decompose every k-connected graph along k-separators into smaller pieces that are (k + 1)-connected or 'basic'. The first step k = 1 is given by the block-cutvertex decomposition. For k = 2, the solution is a classical theorem of Tutte from 1966, which builds on earlier works of Whitney from the 1930s. It was long believed that Tutte's Theorem cannot be fully extended to higher connectivity. I proposed a new perspective on graph connectivity that allowed me to prove a Tutte-Theorem for k = 3 with Carmesin (FOCS 2023), and then for k = 4 with Planken (SODA 2026). Most recently, together with Bourneuf, Carmesin and Planken, we found an approximate solution for all k: an approximate cactus-decomposition for vertex-connectivity. Like the classical cactus of Dinitz, Karzanov and Lomonosov (1976), which represents all minimum edge-cuts of a graph, it represents all minimum vertex-cuts, up to a bounded number of vertices.

Local-global invariants of graphs and groups

The question to what extent graph invariants – the chromatic number, say, or connectivity – are of local or global character, and how their local and global aspects interact, drives much of the research in graph theory both structural and extremal. This project offers such studies a possible formal basis. Tree-decompositions display the global structure of a graph when it resembles a tree, but large sparse networks such as road networks typically do not. With colleagues, I have developed a framework of graph-decompositions along r-local separators: vertex sets that separate the ball of diameter r around them, but not necessarily the entire graph. In a road network, these are the bottlenecks that are prone to congestion. In our main paper with Diestel, Jacobs and Knappe (Transactions of the AMS 2026), we combine coverings, as known from Topology, with tangle-tree decompositions, as known from Graph Minor Theory, to canonically decompose finite graphs and groups into their r-locally highly connected regions. In a follow-up paper with Jacobs and Knappe, we describe these decompositions directly in the finite graph. I am currently working on applications in Theoretical Computer Science and Combinatorial Group Theory.

The Farey graph

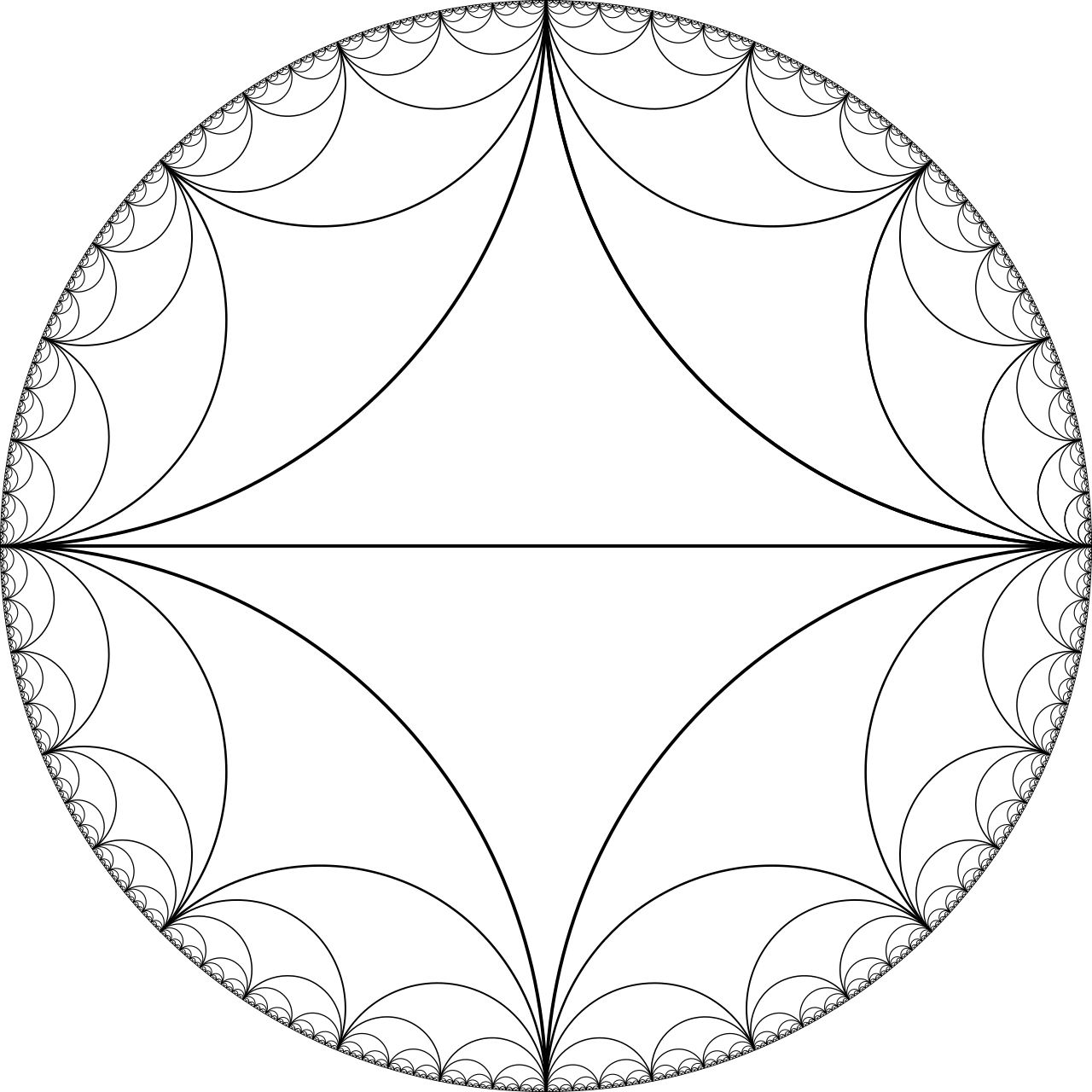Farey graph

The Farey graph, shown on the left and surveyed on 300 pages in Hatcher's new book (PDF), plays a role in a number of mathematical fields ranging from group theory and number theory to geometry and dynamics. Curiously, graph theory has not been among these until very recently, when I showed that the Farey graph plays a central role in graph theory too: it is one of two infinitely edge-connected graphs that must occur as a minor in every infinitely edge-connected graph. Previously it was not known that there was any set of graphs determining infinite edge-connectivity by forming a minor-minimal list in this way, let alone a finite set. This result marked the starting point of a project in which I addressed exciting follow-up questions.

The whirl graph

The whirl graph on the left answers three questions about the Farey graph at once. For instance, the whirl graph is infinitely edge-connected and contains the Farey graph as a minor with branch sets of size two, but it does not contain a subdivision of the Farey graph. In fact, the whirl graph contains no subdivision of any naively constructed infinitely edge-connected graph, because it has the following property: For any two vertices u,v and any positive integer k, the whirl graph contains k edge-disjoint order-compatible u–v paths but not infinitely many.

Publications and preprints

Cactus-decompositions for all levels of connectivity

Local-global invariants of graphs and groups

Combinatorics in 3D

Farey graph

End spaces

Star-comb series

Ends and tangles

Theses